النظام العددي الثنائي Binary system
الحاسوب, ذلك الجهاز الذي يقوم بتلك الحسابات الخارقة, ويقوم بالتخزين والاسترجاع, والمحاكاة والتنفيذ, ذلك الجهاز الذي قلما تجد منزلاً لا يحتويه, الذي أصبح ضرورة من ضروريات الحياة اليومية ! , ألم تتساءل يوماً: " سبحان الله, كيف يقوم بكل هذا ؟"
في موضوعنا هذا, سنتحدث بشكل مُبسط ومختصر عن أهم أساسيات عمل الحاسب الآلي, وهي الأعداد الثنائية (Binary number ), والتي تعتبر – تجاوزاً – لغة الحاسب الآلي, فكما يوجد للعرب لغة تتكون أبجدياتها من 28 حرفاً ( أ – ي ) , وللإنجليز لغة تتكون أبجدياتها من 26 حرفاً ( A – Z ) , كذلك الحاسب يمتلك لغة تتكون أبجدياتها من حرفين ( 0 , 1 ) , أو ( ON , OFF ) , أو بمعنى أكثر وضوحاً ( يوجد تيار , لا يوجد تيار ), وهذه اللغة كما ذكرنا تعرف باسم: الأعداد الثنائية...
* تمثيل الأعداد الثنائية:
أعتقد الآن أنك تتساءل: " ماذا يعني للحاسب يوجد تيار أم لا ؟ وماذا يفهم من ذلك ؟ " , في الحقيقة كما هو الحال في لغة العرب فالألف لوحدها قد لا تعني شيئاً وكذلك الحال مع أختها الباء, ولكن عندما نجمعهم سويةً تتشكل لنا جملة مفهومة عند العرب وهي (أب) , وكذلك هو الحال مع الحاسب فمن خلال تشكيل مجموعة من الـ(1 , 0 ( يتمثل لنا رقم أو كلمة معينة, فعلى سبيل المثال: عندما نريد تمثيل العدد واحد بواسطة الأعداد الثنائية فإنه يتم تمثيله بهذا الشكل ( 01 )...
ومما تجدر الإشارة إليه, إننا عندما نريد أن نمثل عدداً ما, فإننا نكون محصورين بعدد معين من الـBit , وكل واحد أو صفر هو في الحقيقة عبارة عن ( one bit ) , وللتوضيح أكثر سنمثل الآن العدد واحد بواسطة ( 5 bit ) والتي ستكون بالشكل التالي (00001)
كما ذكرنا, إننا محصورين بعدد معين من الـBit عندما نريد تمثيل عدداً ما, وليتضح الموضوع بشكل أكبر الآن سنمثل العدد 15 بالأرقام الثنائية والتي تكون كالتالي (1111) , نلاحظ إنه تم تمثيلها بواسطة (4 bit) , إذاً عندما أطلب منك أن تمثل لي العدد 15 بواسطة (3 bit) هل تستطيع ؟ .. في الحقيقة لا تستطيع وذلك لأنك لا تمتلك عدداً كافياً من الـBit, فكما لاحظنا إن العدد 15 يحتاج إلى (4 bit) أو أكثر لتمثيله لذا الـ(3 bit) لا تستطيع أن تقوم بهذه العملية...
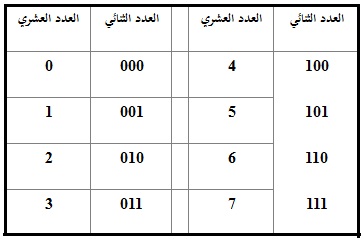
قد تتساءل: " كيف لي أن أعرف الأعداد التي أستطيع تمثيلها بواسطة عدد معين من الـBit ؟ " , هناك معادلة رياضية بسيطة للإجابة على هذا السؤال, فمثلاً: عندما يكون لديك ( n bit ) حيث n هو رقم موجب متغير, فإنك تستطيع تمثيل الأعداد من العدد صفر إلى العدد (2^n) – 1, - حيث علامة ^ تعني مرفوع إلى الأس n - ولنجرب مثالاً عملياً على ذلك, ولنفرض إننا نريد أن نعرف الأعداد التي نستطيع تمثيلها بواسطة ( 3 bit ), فمن خلال المعادلة نجد إنها من العدد صفر إلى العدد سبعة...
- الأرقام الثنائية التي نستطيع تمثيلها بواسطة (3 bit -
* من الثنائي إلى العشري:
والآن قد تتساءل لتقول: " ما هذا ؟ كيف سأحفظ مجموعات مكونة من الصفر والواحد لأعرف ماذا تعني؟ ", نجيبك بهدوء لنقول لك: يا أخي العزيز هّون عليك فليس هناك داعٍ للحفظ, توجد هناك عملية حسابية صغيرة نستطيع من خلالها معرفة العدد العشري من العدد الثنائي, ولنأخذ على سبيل المثال هذا العدد الثنائي (011001), في الحقيقة أنا الآن لا أعلم ماذا يُمثل هذا الرقم في الأعداد العشرية ! , ولكن أنا وأنت بعد قليل سنكتشف ماذا يمثل هذا الرقم, بالطريقة التالية:-
كما ترى, العملية بسيطة جداً, مجرد حسابات بالطريقة ذاتها مع إي رقم ثنائي أخر , ولتثبيت المعلومات سنقوم بهذه العملية مع العدد الثنائي (1111) والذي قلنا سابقاً إنه يمثل العدد 15 , لنرى هل ما قلناه كان صحيحاً أم لا ؟...
2^3 + 2^2 + 2^1 + 2^0 = 8 + 4 + 2 + 1 = 15
* من العشري للثنائي:
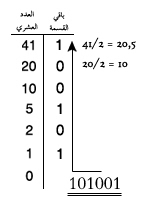
جميل جداً, ولكن بالتأكيد سنواجه مشكلة أخرى وهي: كيفية معرفة العدد الثنائي الذي يمثله ذلك العدد العشري؟, ولكن لا تخف بواسطة عمليات قسمة بسيطة نستطيع استخلاص العدد الثنائي من العشري, وذلك بقسمة العدد العشري على اثنين, في حالة لا يوجد باقي للقسمة يصبح العدد صفر, وفي حالة وجود باقي للقسمة يصبح العدد واحد, وهكذا نكرر عملية القسمة إلى أن نصل إلى الناتج صفر..أعلم إن الموضوع يبدو معقداً قليلاً , ولكن بالمثال العملي التالي ستتضح الفكرة – بأذن الله -, ولنفرض إننا نريد معرفة العدد الثنائي الذي يمثل العدد 41 , ببساطة نقوم بعمليات القسمة السابق ذكرها للحصول على الناتج:
كما رأينا, الطريقة بسيطة جداً والأمر مماثل لأي عدد عشري أخر نرغب في تمثيله ثنائياً, ولتأكد من صحة الحل نقوم بطريقة التحويل من العدد الثنائي للعشري للناتج الذي حصلنا ( 101001 ) عليه لنرى هل هو مطابق للعد 41 أم لا ؟ , وعند تطبيق هذه الطريقة نجد إن الناتج عبارة عن جمع لـ( 32 + 8 + 1) والذي يكافئ العدد 41...
* جمع الأعداد الثنائية:
والآن بعد أن تعرفنا على مجموعة من أهم الأساسيات في عالم الأعداد الثنائية, سننتقل إلى واحدة من أهم العمليات التي يُمكن تطبيقها على الأعداد الثنائية وهي عملية ( الجمع ) , فلنفرض مثلاً إن لدينا ( 3 bit ) وإننا نريد أن نجمع العدد 1 مع العدد 2 بواسطة الأرقام الثنائية, وأيضاً نريد أن نجمع العدد 3 مع العدد 3, كيف نقوم بهذه العملية ؟..ببساطة, نقوم بالطريقة التالية:

ماذا حدث؟ في المثال الأول ( 1 + 2 ) , أضفنا ( 1 + 0 = 1 ) , وأيضاً ( 0 + 1 = 1 ) , وأخيراً ( 0 + 0 = 0 ) , وبالتالي أصبح الناتج ( 011 ) , ولكن ماذا حدث في المثال الآخر ؟ أولاً ( 1 + 1 = 2 ) ولكن كيف؟ لا يوجد الرقم 2 في الأعداد الثنائية ! , إذاً لنراجع معاً كيفية الجمع في الأعداد العشرية ولنجمع مثلاً: 19 + 11 , في المرة الأولى نجمع (9+1=10) , ولكن في الحقيقة نحن نضع 0 , ويبقى معنا في اليد واحد نضيفه في عملية الجمع التالية والتي هي ( 1 + 1 = 2) , ونضيف عليها الـ1 الذي معنا باليد فيصبح لدينا العدد (30) , وكذلك نفعل مع الأعداد الثنائية ( 1 + 1 = 0 ) ولكن يبقى معنا واحد نضيفه في عملية الجمع التالية والتي هي ( 1 + 1 + 1 = 1 ) وكذلك يبقى لدينا في اليد واحد نضيفه في عملية الجمع التالية ( 0 + 0 + 1 = 1 ) , وهاهي الطريقة مع أي عدد ثنائي آخر...
* تمثيل الأعداد الثنائية السالبة:
تحدثنا عن الأعداد الثنائية ( الموجبة ) , ولكن ماذا عن الأعداد السالبة ؟ , هناك ثلاثة طرق للتعامل مع الأعداد الثنائية السالبة وهي ( sign magnitude ) , ( one's complement ) , ( two's complement ) , سنتحدث الآن عن الطريقة المُثلى للتعامل وهي الأخيرة (two's complement ), والتي سنقوم بالتعامل معها بالشكل التالي:
نقوم بتمثيل العدد الموجب أولاً ( بالطريقة السابقة ) , ومن ثم نقوم بقلب جميع الأعداد ( الصفر للواحد , الواحد للصفر ), وأخيراً نُضيف إليها واحد فنحصل بالتالي على تمثيل العدد السالب, وليتضح الأمر لنفرض إننا نريد تمثيل العدد ( -1 ) والعدد (-3) بواسطة ( 3 bit ) – أنظر للشكل التالي - :
كما رأينا, الطريقة ثابتة مع أي عدد ثنائي أخر نرغب في تمثيله بالشكل السالب, ولكن هناك عدد من الملاحظات المهمة أثناء تعاملنا مع الأعداد السالبة والتي لابد أن تنتبه لها وهي كالآتي:-
- كما رأينا في تمثيل الأعداد الثنائية الموجبة, كنا محصورين بعدد معين من الـbit , وتعرفنا على المعادلة التي تخبرنا بالأعداد التي نستطيع تمثليها بواسطة عدد معين من الـbit , في تمثيل الأعداد الثنائية السالبة سيتكرر الأمر ذاته, ولكن مع اختلاف طفيف بالمعادلة , لماذا ؟ .. لأننا بواسطة ذلك العدد من الـbit , لن نُمثل فقط الأعداد الموجبة , ولكن سنقوم بتمثيل الأعداد الموجبة والسالبة معاً وذلك باستخدام المعادلة التالية: ولنفرض إن لدينا (n bit) , إذاً الأعداد التي نستطيع تمثيلها هي:
من ( -2^(n-1) ) إلى ( 2^(n-1) – 1 ), ذلك يعني إن الأعداد التي نستطيع تمثيلها بواسطة (3 bit) في الـ(two's complement ), هي من: ( -2^2 ) إلى ( ( 2^2) – 1) أي: من -4 إلى 3 , ونلاحظ هنا الاختلاف بين تمثيل الأعداد الموجبة والسالبة, حيث كانت الأعداد التي نستطيع تمثيلها بواسطة (3bit) في الأعداد الموجبة هي: من 0 إلى 7
- في نظام الـ(two's complement ), نستطيع تمييز هل العدد سالب أم موجب من خلال النظر إلى الخانة الأولى من اليسار, فإن كان الرقم بـ0 , فهو في الحقيقة يمثل عدد موجب, وإن كان الرقم بـ1 , فإنه يمثل عدداً سالباً..
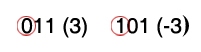
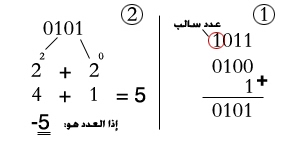
- لنستطيع معرفة العدد الثنائي السالب ماذا يمثل في النظام العشري, لا نستطيع استخدام الطريقة التي تعرضنا لها سابقاً (التحويل من ثنائي لعشري ) مباشرةً , ولكن نرى إن كان العدد سالباً ( بالنظر إلى أول خانة على اليسار كما ذكرنا ) , نقوم بعملية الـ(two's complement ) له, وذلك من خلال القلب والإضافة بواحد – كما ذكرنا – لنحصل على العدد الموجب الذي يمثله ذلك العدد السالب, وبعد ذلك نقوم بالعملية السالف ذكرها وهي: التحويل من ثنائي لعشري, فعلى سبيل المثال نريد أن نعرف العدد السالب التالي ( 1011 ) ماذا يمثل؟ -- أنظر للشكل التالي:
- أخيراً, انتبه ألا تختلط عليك الأمور, فمثلاً عندما أسالك ماذا يمثل العدد التالي ( 111 ) , في الحقيقة الأمر يعتمد على النظام الذي تتعامل معه, فعندما تتعامل مع أرقام ثنائية موجبة فقط فالعدد السابق يمثل العدد 7 , بينما يمثل العدد -1 في نظام الـ(two's complement ) -كما رأينا سابقاً -
بينما العدد 7 نمثله بالـ(two's complement ), بالشكل التالي (0111), وبالتالي يجب أن تعرف أولاً مع أي نظام تعمل, لتستطيع التعامل مع الأرقام بالشكل الصحيح..
- قد تتساءل: " لماذا تعاملنا في بادئ الأمر مع الأعداد الثنائية الموجبة, والآن تعاملنا مع الأعداد الثنائية السالبة, ألا يجدر بنا أن نتعامل معهم بطريقة واحدة ؟ " , في الحقيقة هناك أنظمة لا تحتاج إلى أعداد ثنائية سالبة, وبالتالي نحن نحجز مساحة للأعداد الثنائية السالبة وهي في الحقيقة لن تستخدم, وبمعنى أوضح: كما ذكرنا سابقاً الـ(3 bit) في الأعداد الثنائية الموجبة نستطيع تمثيل الأعداد فيها إلى العدد 7, بينما عندما نتعامل مع نظام الـ(two's complement ), لن نستطيع تمثيل إلا للعدد 3 ! , وليصبح الموضوع أكثر وضوحاً, تخيل معي أنك مهندسٌ إلكتروني وطُلب منك أن تُصمم آلة حاسبة, بالتأكيد ستقوم باستعمال نظام الـ(two's complement ), لأن آلتك الحاسبة ستحتاج إلى أعداد موجبة وسالبة, بينما تخيل لو إنه طُلب منك أن تصمم ساعة إلكترونية, بالتأكيد ستتعامل مع الأعداد الثنائية الموجبة فقط, ومن هنا يكمن الفرق...





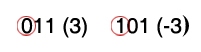
ليست هناك تعليقات:
إرسال تعليق